2013.04.19. 11:20
Guesstimation – becslés adatok nélkül (2. rész)
A becslési feladatok időnként egészen elvontak is lehetnek. Ahogy már említettük, a tanácsadó cégek előszeretettel használnak úgynevezett guesstimation, azaz adatok nélküli becslésre épülő feladatokat az állásinterjún. Mivel a klasszikus feladatokra (pl. piacbecslés, nyereségesség becslése) elég jól fel lehet készülni, így a cégek elkezdtek nehezebben megfogható témákat adni a jelentkezőknek. Cikksorozatunk második részében egy ilyen, kissé elvont becslési feladatot fogunk megoldani - először a nehéz, utána a könnyű úton.
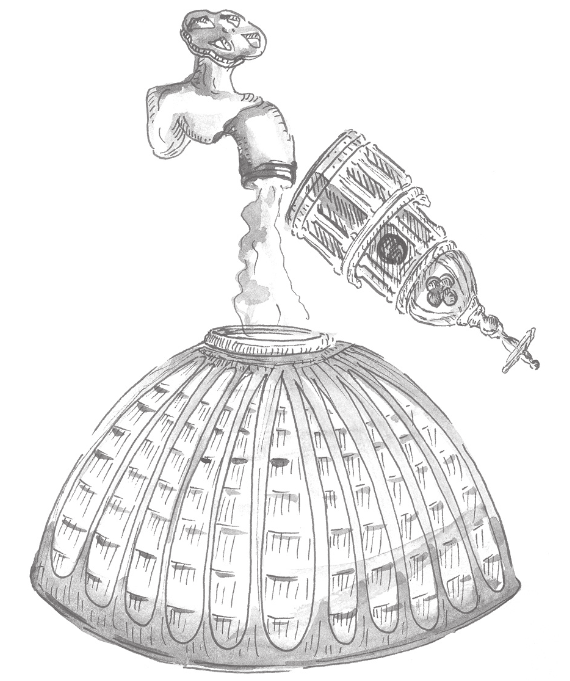
A fealadat a következő. Adott a Szent István Bazilika kupolája. Mennyi időbe telne egy csap segítségével megtölteni vízzel a (megfordított) kupolát?
Brute force
Nézzük először a nehéz módszert. Ugye két dolgot kell kiszámolnunk: egyrészt a kupola térfogatát, másrészt egy átlagos csap átfolyási sebességét. A kupola térfogatához szükségünk van a sugarára. Ezt valószínűleg nem tudjuk fejből, de egy durva becsléssel azt mondhatjuk, hogy 20 méter. A kupola megközelítőleg egy félgömb alakú test, tehát a térfogat (a középiskolában tanult képlettel, amire minden bizonnyal még emlékezünk):
Remek. Mivel egy m3 1000 liter víznek felel meg, így a térfogatot még meg kell szoroznunk 1000-rel, tehát összesen 6,000,000 liter vízre van szükség a kupola megtöltéséhez. A következő lépés a csap átfolyási sebsségének meghatározása. Aki szokott felmosni, az tudja, hogy egy 10 literes vödröt kb. egy perc alatt lehet megtölteni vízzel. Számoljunk ezzel.
A fenti osztás segítségével megkapjuk, hogy 600,000 perc, azaz nagyjából egy év szükséges ahhoz, hogy egy csap feltöltse a Bazilika kupoláját vízzel. A brute force módszer tehát működik, de igen sok számolást igényel.
Absztrakció
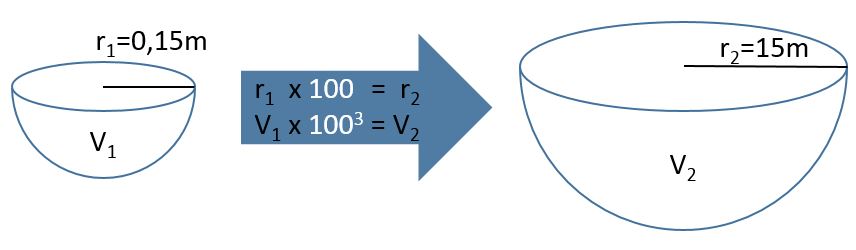
Most pedig következzen egy sokkal egyszerűbb módszer, ami az absztrakció erejére épít. Ehhez el kell vonatkoztatnunk az eredeti problémától, és egyszerűsítési lehetőséget kell keresnünk. A kupola félgömb alakú, a térfogat képlete pedig fejszámolásnál nehézséget okozhat. Ha magát a képletet ki tudnánk küszöbölni, máris egyszerűbb lenne a helyzet. A mosdókagyló tulajdonképpen szintén egy félgömbhöz hasonló test, ezért felhasználhatjuk összehasonlítás céljából. A sugara kb. 15 cm. Borotválkozás előtt kb. fél percig tart megtölteni a csappal a mosdókagylót. Tehát tudjuk, hogy egy 15 cm sugarú félgömb feltöltése fél perc. A gömb képletében a sugár köbös formában szerepel, tehát két félgömb térfogata a sugarak hányadosának köbével arányos. Magyarul: a kupola 100-szoros sugara azt jelenti, hogy a kupolát nem fél, hanem 100 x 100 x 100 x 0,5 perc alatt lehet megtölteni vízzel. Ez 500,000 perc, azaz körülbelül egy év.
Melyik módszer a jobb?
Mint láthatjuk, a két megközelítés hasonló eredményt hoz, de a második sokkal kevesebb számolást igényel, gyorsabb. A végeredmények eltérése miatt sem kell aggódnunk, hiszen a becslés nem a pontos adatokról szól. Ha belegondolunk, egy mosdókagyló a legtöbb esetben nem félgömb alakú.
Ezzel kapcsolatban felmerül a kérdés, hogy vajon melyik módszer a jobb. Nos, attól függ. Az absztrakció egy elegánsabb megoldás, amivel kitűnhetünk a jelentkezők sorából. Az is igaz ugyanakkor, hogy nem minden feladatot lehet megoldani ilyen trükkökkel, és ha meg is lehet, nem biztos, hogy egy stresszes szituációban épp eszünkbe fog jutni egy. Összességében tehát egy esetinterjún érdemes néhány másodpercig gondolkodni, és ha nem ugrik be a nagy ötlet, akkor brute force módszerrel megoldani a hasonló feladatokat.
Ajánlott irodalom
Weinstein, A., Adam, J.A. (2008). Guesstimation: Solving the World's Problems on the Back of a Cocktail Napkin. Princeton University Press. Megjegyzés: a fenti példa és a brute force megoldás ebből a könyvből származik. Az absztrakciós megoldás a cikk szerzőjének műve.
Hubbard, D.W. (2010). How to Measure Anything: Finding the Value of Intangibles in Business. Wiley.