A becslési feladatok időnként egészen elvontak is lehetnek. Ahogy már említettük, a tanácsadó cégek előszeretettel használnak úgynevezett guesstimation, azaz adatok nélküli becslésre épülő feladatokat az állásinterjún. Mivel a klasszikus feladatokra (pl. piacbecslés, nyereségesség becslése) elég jól fel lehet készülni, így a cégek elkezdtek nehezebben megfogható témákat adni a jelentkezőknek. Cikksorozatunk második részében egy ilyen, kissé elvont becslési feladatot fogunk megoldani - először a nehéz, utána a könnyű úton.

A fealadat a következő. Adott a Szent István Bazilika kupolája. Mennyi időbe telne egy csap segítségével megtölteni vízzel a (megfordított) kupolát?

Brute force

Nézzük először a nehéz módszert. Ugye két dolgot kell kiszámolnunk: egyrészt a kupola térfogatát, másrészt egy átlagos csap átfolyási sebességét. A kupola térfogatához szükségünk van a sugarára. Ezt valószínűleg nem tudjuk fejből, de egy durva becsléssel azt mondhatjuk, hogy 20 méter. A kupola megközelítőleg egy félgömb alakú test, tehát a térfogat (a középiskolában tanult képlettel, amire minden bizonnyal még emlékezünk): 

Remek. Mivel egy m3 1000 liter víznek felel meg, így a térfogatot még meg kell szoroznunk 1000-rel, tehát összesen 6,000,000 liter vízre van szükség a kupola megtöltéséhez. A következő lépés a csap átfolyási sebsségének meghatározása. Aki szokott felmosni, az tudja, hogy egy 10 literes vödröt kb. egy perc alatt lehet megtölteni vízzel. Számoljunk ezzel.

A fenti osztás segítségével megkapjuk, hogy 600,000 perc, azaz nagyjából egy év szükséges ahhoz, hogy egy csap feltöltse a Bazilika kupoláját vízzel. A brute force módszer tehát működik, de igen sok számolást igényel.

Absztrakció

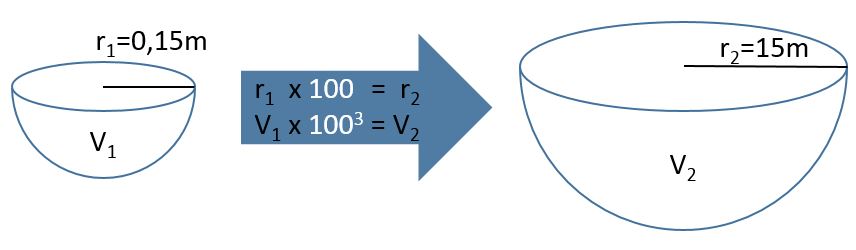
Most pedig következzen egy sokkal egyszerűbb módszer, ami az absztrakció erejére épít. Ehhez el kell vonatkoztatnunk az eredeti problémától, és egyszerűsítési lehetőséget kell keresnünk. A kupola félgömb alakú, a térfogat képlete pedig fejszámolásnál nehézséget okozhat. Ha magát a képletet ki tudnánk küszöbölni, máris egyszerűbb lenne a helyzet. A mosdókagyló tulajdonképpen szintén egy félgömbhöz hasonló test, ezért felhasználhatjuk összehasonlítás céljából. A sugara kb. 15 cm. Borotválkozás előtt kb. fél percig tart megtölteni a csappal a mosdókagylót. Tehát tudjuk, hogy egy 15 cm sugarú félgömb feltöltése fél perc. A gömb képletében a sugár köbös formában szerepel, tehát két félgömb térfogata a sugarak hányadosának köbével arányos. Magyarul: a kupola 100-szoros sugara azt jelenti, hogy a kupolát nem fél, hanem 100 x 100 x 100 x 0,5 perc alatt lehet megtölteni vízzel. Ez 500,000 perc, azaz körülbelül egy év.

Melyik módszer a jobb?

Mint láthatjuk, a két megközelítés hasonló eredményt hoz, de a második sokkal kevesebb számolást igényel, gyorsabb. A végeredmények eltérése miatt sem kell aggódnunk, hiszen a becslés nem a pontos adatokról szól. Ha belegondolunk, egy mosdókagyló a legtöbb esetben nem félgömb alakú.

Ezzel kapcsolatban felmerül a kérdés, hogy vajon melyik módszer a jobb. Nos, attól függ. Az absztrakció egy elegánsabb megoldás, amivel kitűnhetünk a jelentkezők sorából. Az is igaz ugyanakkor, hogy nem minden feladatot lehet megoldani ilyen trükkökkel, és ha meg is lehet, nem biztos, hogy egy stresszes szituációban épp eszünkbe fog jutni egy. Összességében tehát egy esetinterjún érdemes néhány másodpercig gondolkodni, és ha nem ugrik be a nagy ötlet, akkor brute force módszerrel megoldani a hasonló feladatokat.

Ajánlott irodalom

Weinstein, A., Adam, J.A. (2008). Guesstimation: Solving the World's Problems on the Back of a Cocktail Napkin. Princeton University Press. Megjegyzés: a fenti példa és a brute force megoldás ebből a könyvből származik. Az absztrakciós megoldás a cikk szerzőjének műve.

Hubbard, D.W. (2010). How to Measure Anything: Finding the Value of Intangibles in Business. Wiley.

A hőn áhított tanácsadó cég állásinterjúján ülsz, és igyekszel a legjobb formádat hozni. A célod: meggyőzni a veled szemben ülőt, hogy Te vagy a legjobb. Az első tíz percben minden rendben ment: kezet fogtatok, elmesélted az eddigi eredményeid és sikerült nem leönteni magad a meglepően könnyű pohárban lévő vízzel. Most viszont kaptál egy kérdést, amivel nem tudsz mit kezdeni: Hány ember ül éppen repülőgépen az USA-ban. Ezer? Nem, annál biztos több. Egymillió? Á, az túl sok. A fenébe, fogalmam sincs… Inkább iszok egy kis vizet, hátha azalatt megjön az ihlet.

Egy ilyen helyzetben általában nem segít az időhúzás. A legtöbb embernek szüksége van arra, hogy tudatosan készüljön a hasonló, állásinterjún feltett becslős kérdésekre. De miért is tesznek fel ilyen kérdéseket a cégek, és hogyan lehet ezeket megválaszolni? Cikksorozatunk első részében ezekre a kérdésekre keressük a választ.

Miért?

A becslős kérdésekkel kiválóan lehet tesztelni a jelentkezők analitikus gondolkodásmódját, illetve a számolási affinitásukat. Egy tanácsadó cégnél ezek nagyon keresett értékek, hiszen az ügyfélnek mindent számokkal kell alátámasztani. Az adatok azonban nem mindig állnak rendelkezésre, mivel például a jövőre vonatkoznak. Ilyenkor jön képbe a becslés, vagy találó angol kifejezéssel: a guesstimation.

A becslést általában nem tanítják az iskolákban. Sőt, amikor számokról van szó, az uralkodó nézet a precíziót részesíti előnyben: a jó adat a pontos adat. A becslések azonban természetüknél fogva nem ilyenek. A fenti példánál maradva, az állásinterjúkon a legtöbbször csak annyit várnak el, hogy a végeredmény nagyságrendileg helyes legyen (in the ballpark).

Hogyan?

Az előzőeknek megfelelően az Amerika felett épp repülőn ülő személyek számánál sem egy pontos végeredményt vár az interjúztató. Ebből következik, hogy néhány egyszerű művelettel megbecsülhető ez a szám. A gyakorlatban két módszert, a felülről és az alulról becslést érdemes használni.

A felülről való becslés (top-down) egy nagyobb számból indul ki, és osztással illetve kivonással jut el az eredményhez. Induljunk ki az Egyesült Államok lakosságából, ami durván 300 millió főt jelent. Már csak azt kell megtudnunk, hogy ennek mekkora része van a levegőben. Nézzük: az átlag amerikai valamivel gyakrabban repül, mint egy magyar, számoljunk mondjuk évi három úttal. Egy út átlagosan kb. három órás, tehát egy amerikai kilenc órát tölt évente a levegőben. Egy év közel 9000 órából áll (24 x 365), tehát egy átlag amerikai az ideje 0,1%-át tölti a levegőben évente. Mivel végig átlagokról beszéltünk, ezért ezt rávetíthetjük a teljes népességre, tehát a jelen pillanatban az USA felett repülőn ülők száma 300 millió x 0,1% = 300 ezer. A becslésünk tehát 300 ezer, ami reálisnak is tűnik.

Az alulról való becslés (bottom-up) ezzel szemben kis számokból építkezik, szorzással és összeadással. Az Egyesült Államoknak 50 állama van, államonként mondjuk két jelentősebb repülőtérrel, ez összesen 100. Egy reptérről óránként felszáll kb. 10 gép. Egy repülőgépben kb. 150 férőhely van (25 sor x 6 szék/sor), az átlagos kihasználtság pedig durván 2/3-os, tehát repülőnként számolhatunk 100 fővel. Azt pedig már az előbb is felhasználtuk, hogy egy átlag repülőút időtartama három óra. Ezt összeszorozva 100 x 10 x 100 x 3 = 300 ezer főt kapunk.

A fenti két módszer ugyanazt a végeredményt adta, ám általában érdemes a bottom-up módszert használni. Ez valamivel időigényesebb lehet, de a végeredmény az esetek többségében pontosabb. Az is igaz persze, hogy bonyolultabb problémáknál a két módszer keverésére van szükség. Például a fenti felülről becslős példánál is be kellett vetni a bottom-up módszert, hogy megtudjuk, mennyi időt tölt egy átlag amerikai a levegőben évente.

Mikor?

A guesstimation számos olyan helyzetben alkalmazható, amikor gyorsan, adatok nélkül szeretnénk kiszámolni valamit. Tipikusan ilyenek a bevezetőben is említett esetinterjúk, vagy éppen az esetversenyek, ahol egy javasolt termék eredményre gyakorolt hatását (bevétel, kiadás) szeretnénk megbecsülni. Ez pedig már gyakorlatilag üzleti tervezést jelent, amely területen szintén szükség van becslésekre, bár az adatok forrása sok esetben benchmark (pl. iparági átlagok). A cikkíróhoz hasonló mazochisták pedig a mindennapi életben is szórakoztathatják magukat illetve ismerőseiket hasonló becslős feladatokkal :)

Már meglepően kevés gyakorlással is magabiztos rutinra tehetünk szert a becslések terén. Az esetinterjúkon az igazi ellenség sokkal inkább a kínos pillanatokat okozó könnyű poharakban keresendő.

Ajánlott irodalom

Weinstein, A., Adam, J.A. (2008). Guesstimation: Solving the World's Problems on the Back of a Cocktail Napkin. Princeton University Press.

Hubbard, D.W. (2010).How to Measure Anything: Finding the Value of Intangibles in Business. Wiley.